数字三角形模型 闫氏dp法

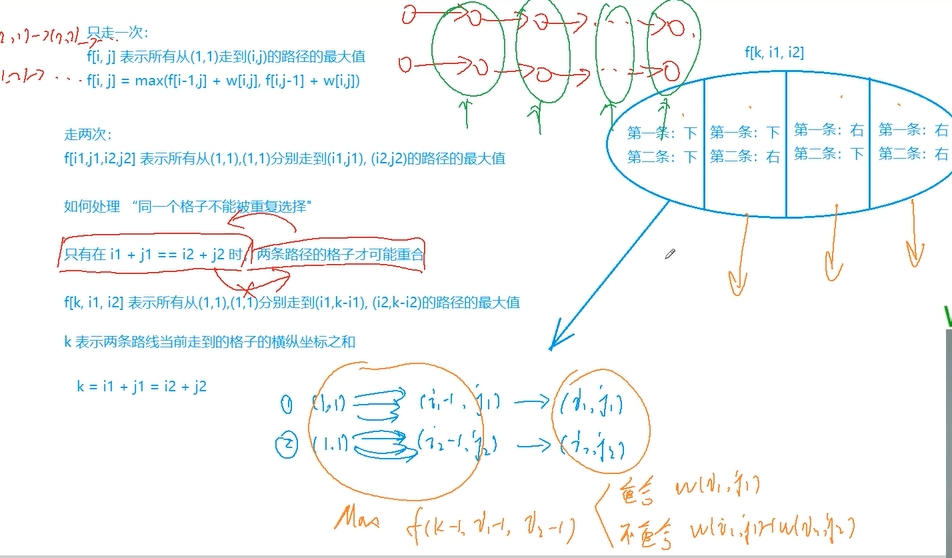
此题和传统的题不一 是同时走两条路径 并且每个格子里的数只能用一次

判断两条路径重合 只有在i1 + j1 = i2 + j2 的时候才有可能 但是 反之不然 感兴趣的同学可以画图试试

相关思路图上很清楚 那就直接上代码：

Code：

#include <iostream>
#include <algorithm>
#include <cstring>
#define int long long  //个人习惯 有备无患

using namespace std;
const int N = 15;
int g[N][N];
int f[N * N][N][N];   //动态规划数组
int n;

signed main()
{
    cin >> n;
    int a , b , c;
    while (cin >> a >> b >> c , a || b || c) g[a][b] = c;  //abc为零 停止输入

    for (int k = 2 ; k <= n + n ; k ++ )
    {
        for (int i1 = 1 ; i1 <= n ; i1 ++ )
        {
            for (int i2 = 1 ; i2 <= n ; i2 ++ )
            {
                int j1 = k - i1 , j2 = k - i2;
                if (j1 >= 1 && j1 <= n && j2 >= 1 && j2 <= n)
                {
                    int t = g[i1][j1];
                    if (i1 != i2) t += g[i2][j2];
                    int &x = f[k][i1][i2];  //&x代表一个临时的三位数组 懒得写这么长了
                    x = max(x , f[k - 1][i1 - 1][i2 - 1] + t); //状态转移
                    x = max(x , f[k - 1][i1 - 1][i2] + t);
                    x = max(x , f[k - 1][i1][i2 - 1] + t);
                    x = max(x , f[k - 1][i1][i2] + t);
                }
            }
        }
    }
    
    cout << f[n + n][n][n] << endl;

    return 0;
}

题解不宜 求赞orz